Analyse du Battement

(A.JABES)

        

                                                       

 

 

Cette étude porte aussi bien sur des mécanismes simples, destinés à des modèles réduits, que  sur des mouvements plus complexes, transposables à des appareils grandeur.

 

LE BATTEMENT

 

THÉORIE

 

A- MOUVEMENT RECTILIGNE.

 

Prenons le cas d'une aile d'un seul tenant et faisons la battre de la manière suivante:

1-Mouvement rectiligne de haut en bas et retour Ce qui définit l'AMPLITUDE.

2-Pivotement du profil autour d'un axe parallèle au longeron ,surtout aux points   morts haut et bas. C'est la Variation cyclique de Pas( ou mieux l'assiette).

3-Période de battement ,constante: T secondes ou N BATTEMENTS PAR SECONDES ou HERTZ

4- L'appareil (ou l'oiseau) se déplace en vol horizontal à la vitesse V, peu différente de la vitesse de plané.: V= 4(P/SCz) 1/2.

5- Nous supposons l'écoulement permanent, en régime stationnaire sauf remarques en ce qui concerne les points morts hauts et bas : voir plus loin.

 

 

 

                    

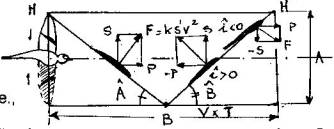
On peut représenter ce mouvement  par le schéma suivant où l'on porte horizontalement la distance parcourue  pendant la période T à la vitesse V et verticalement l'amplitude verticale, parcourue à l'abaissée et à la remontée., à la vitesse V. pendant les temps T/2.                                   

Dans le cas de vol représenté ,on a indiqué les vitesses et les forces appliquées On voit que selon l'incidence de l'aile sur la trajectoire relative(à la remontée),Ies sustentations peuvent, soit s'ajouter,(vol normal),soit se retrancher (vol descendant rapide)

On démontre que la condition nécessaire pour que la sustentation soit positive à la fin  d'un cycle est que  Â< ^B.

 

Ceci peut être obtenu de différentes manières :

 

1°  Cas où le temps d'abaissée : t1 est égal au temps de relevée t2.avec t1+t2 = T.

a) Le corps peut être cabré, comme c'est le cas lors du décollage:

on est alors dans le cas de figure suivant

 

              t1=t2=T/2         

 

 

 

 

 

 

où b) L'aile bat ,dans un plan incliné faisant un angle C avec l'horizontale ,le corps restant horizontal. Le cas de figure correspondant est alors :

 

 

 

 

 

 

 

 

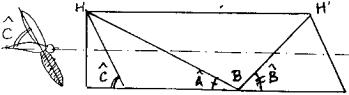
T1=T2=T/2

 

 

2° Cas où le temps d'abaissée  t1 est plus grand que le temps de relevée t2 :t1 > t2, avec toujours t1+ t2 = T

On a les cas de figures suivantes où l'on retrouve les configurations déjà vues, mais aux effets accentués.

 

 

 

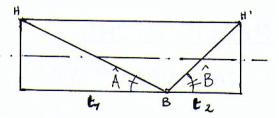
T1>T2

 

 

 

LES PARAMÈTRES DU BATTEMENT

 

D'après plusieurs études ,il ressort qu'à chaque variation brusque de la Circula­tion de vitesse autour du profil d'aile il y a lâcher de tourbillons dans son sillage , en par­ticulier aux points morts hauts et aux points morts bas . En aval de l'aile il y a , dans le cas le plus général un écoulement de tourbillons alternés Ceci a été mis en évidence dans des tunnels hydrodynamiques ( Thèse de Werlé ) et en théorie aérodynamique .

Or ,il existe ,en écoulement régulier de l'aile battante convergence, entre la théorie et l'observation au laboratoire et dans la nature,

 

En effet ,en théorie , Villat dit qu'en régime stable ". le rapport (sans dimensions)

            A/VT=0,28.                 où A est l'Amplitude, V la vitesse horizontale de déplacement et T le temps d'une période.

Ceci est corroboré par l'observation de la nage des poissons: on cite le nombre de Strouhal : A/VT = 0,30.

Enfin, personnellement ,lorsque des valeurs dignes de bonne foi ont pu être utilisées ,soit pour des insectes,soit pour des oiseaux, soit même pour la maquette volante du ptérodactyle de Mac Cready, nous avons trouvé des valeurs très proches de 0,28.

Remarque

 

A/VT=0,28 . Si l'on fait intervenir que A=v.T/2,il s'ensuit que 0,28=v/2V.

 

Cette simplification doit être utilisée avec les plus grandes réserves, mais elle peut per­mettre de définir un projet dans ses grandes lignes.

 

LA VARIATION CYCLIQUE DU PAS

 

En principe l'aile doit suivre la trajectoire relative, avec une incidence normale (3° à 4°. ). D'après Chabonat,  en réalité, les vitesses instantanées sont loin d'être constantes et l'on pourrait fonctionner avec de très grandes incidences, sans risque de décrochage.

 

En restant dans le cadre de cette étude , nous garderons les angles de référence A et B.

   

 

B- MOUVEMENT CIRCULAIRE  ( ou dérivé).

 

 

 

 

 

 

 

 

 

 

 

 

 

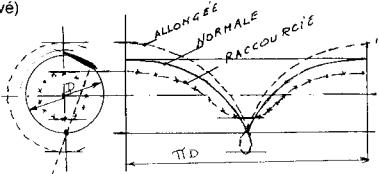
            L’aile  décrit une Cycloide raccourcie ou allongée, selon que la valeur de la vitesse

Horizontale est plus grande ou plus faible que la vitesse tangentielle du cercle générateur.